Современная квантовая механика, как раздел теоретической физики, непрерывно развивается и имеет целый ряд нерешённых задач.

В лаборатории геохимии Луны и планет Института геохимии и аналитической химии им. В.И. Вернадского Российской академии наук (ГЕОХИ РАН), совместно с МФТИ (НИУ) исследовали проблему расходимости энергии вакуума на решётке с теоретико-числовой точки зрения (рис. 1). Полученный результат состоит в том факте, что обнуление энергии вакуума возникает естественным образом на решётке размерностью d=3 и выше для широкого класса рассматриваемых моделей, а именно, если гамильтонианом модели является функция от квадрата импульса. Подобные явления и методы (перенормировки) нужны в получении конечных осмысленных ответов для наблюдаемых величин физических процессов. Результаты опубликованы в журнале p-Adic Numbers, Ultrametric Analysis and Applications.

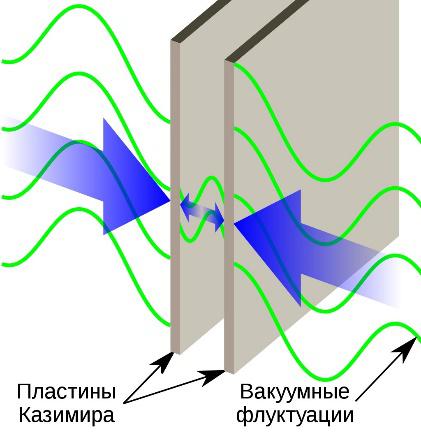
С подсчётом энергии вакуума тесно связана задача о поверхностном натяжении жидкости, где участвуют ван-дер-ваальсовы силы (межмолекулярное взаимодействие). Однако, экспериментально измеренные значения поверхностного натяжения оказываются больше, чем просто разрыв связей между молекулами. Недостающий вклад восполняют квантовомеханические расчёты, которые в этом направлении начались с Хендрика Казимира, вдохновившегося на исследование энергии вакуума после разговора с Нильсом Бором в 1948 году.

Эффекта Казимира (рис. 2) заключается во взаимном притяжении двух проводящих тел под действием квантовых электромагнитных флуктуаций в вакууме как среде. Хотя в наше время его существование и величина экспериментально зафиксированы с высокой точностью, до сих пор существуют разногласия относительно её толкования как неинтуитивного следствия существования вакуума квантовой электродинамики. Замечательно, что, наблюдая геккона (ящерица), бегающего «вверх и вниз по дереву любым способом, даже головой вниз», мы можем видеть в этом эффект Казимира, определяющий многие явления смачивания и прилипания.

Предполагая, что проблема может быть связана с неочевидной особенностью вещественных чисел и операций над ними при квантовании систем, учёные рассмотрели квантовую теорию поля на решётке как более ясный изначальный случай, а не переход от непрерывного пространства к решётке с помощью разностных схем. Квантовая теория поля на решётке размера N строится с естественной для решётки операцией арифметики в кольце Z(N) остатков деления на размер решетки N, тогда не только компоненты импульса, но и энергия пробегают дискретные значения на решётке, причём как проекции импульса, так и энергия рассматриваются как элементы кольца остатков Z(N).

Величина, которую мы называем импульсом (генератор пространственного сдвига на решётке) в физике часто называется квазиимпульсом (с импульсом квазиимпульс совпадает в непрерывном пределе). Аналогично величину, которую мы называем энергией (генератор временно́го сдвига на решётке) можно назвать квазиэнергией.

Поскольку на трёхмерной решётке квазиэнергия вакуума перенормируется в ноль для произвольного размера решётки N, возникает вопрос, можно ли воспользоваться предельным переходом N → ∞, чтобы перейти от квантовой теории поля на решётке к квантовой теории поля в непрерывном пространстве. Можно ли перенести построенную теоретико-числовую перенормировку на непрерывный случай? Есть основания полагать, что такой перенос возможен.

Источник: пресс-служба ГЕОХИ РАН.