Исследование ученых Физико-технологического института им. К. А. Валиева РАН, МФТИ и университета ИТМО позволит создать новые алгоритмы для квантового компьютера. С их помощью можно будет быстрее и эффективнее решать целый ряд практически важных задач: от расчета логистики до разработки новых веществ с нужными свойствами.

«Мы изучаем квантовые блуждания частиц по различным графам, – рассказывает один из авторов исследования ведущий научный сотрудник ФТИАН, преподаватель МФТИ, эксперт РАН Леонид Федичкин.

Леонид Федичкин в лаборатории микроструктурирования и субмикронных приборов ФТИАН.

Граф – это математический объект, представляющий собой множество вершин, соединенных парными связями, которые называются ребрами графов. Физически в реальном мире вершинами графа могут быть, например, атомы в молекуле или квантовые точки в квантовом компьютере, то есть аналоги транзисторов в классическом компьютере. Частица, например – электрон, за счет туннельного эффекта может перемещаться от одной точки до другой вдоль ребер графа.

«Этот процесс важен для различных практических исследований, – рассказывает Леонид Федичкин. – Например, фоточувствительный белок – хлорофилл или родопсин (светочувствительный пигмент глаза) – это очень разветвленная структура, часть которой представляет собой своего рода антенну. Ее задача – поймать фотон. А другая часть белка – это химическая фабрика, где вырабатывается нужное вещество. И задача белковой структуры наиболее эффективным образом доставить энергию возбуждения от уловленного антенной фотона на фабрику. Такой белок, с точки зрения возбужденного электрона, который в нем блуждает, представляет собой очень сложную, разветвленную структуру, настоящий лабиринт, который можно изобразить в виде графа».

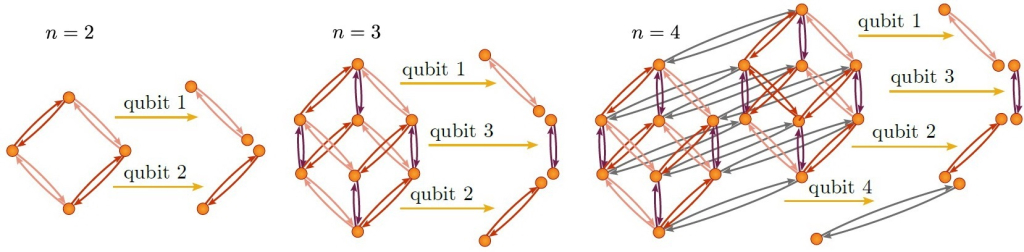
Примеры графов, схематически изображающих квантовый компьютер с 2, 3 и 4 кубитами.

Квантовые блуждания частицы в таком лабиринте отличаются одной важной особенностью, которая лежит в основе преимуществ, которые обещают квантовые компьютеры. Если бы возбужденный электрон был классической частицей, которая ищет путь, перебирая все варианты маршрута, то у него ушло бы столько времени, чтобы добраться до цели, что все его возбуждение к тому моменту уже прошло бы. Однако на самом деле этот процесс происходит в виде квантового блуждания.

«Квантовое блуждание принципиально отличается от блуждания классического, которое больше похоже на диффузию, когда распространение идет примерно пропорционально корню из времени, – говорит Леонид Федичкин. – А квантовое распространение может происходить линейно. То есть для классических частиц время блуждания по "лабиринту" от старта до финиша растет в квадрате от его длины (вернее, числа узлов), а для квантовых частиц – линейно. Собственно, в этом также проявляется превосходство квантовых компьютеров над обычными».

 

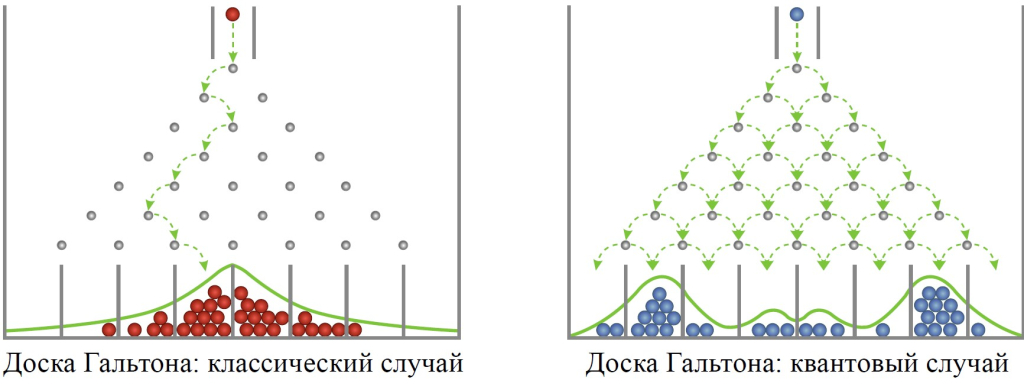
На этом рисунке наглядно представлена различие между поведением классических и квантовых частиц.

Однако для того, чтобы частица перемещалась между вершинами графа квантовым образом, необходима когерентность – то есть согласованность квантовой динамики во всей системе. Но такое состояние может быть только в идеальном случае при полной изоляции системы от внешних влияний. В реальности этого добиться невозможно, поэтому для получения корректной картины исследователи ввели в процесс квантовых блужданий декогеренцию, затухание, то есть разрушение квантовости под влиянием внешнего мира.

Помимо когерентности, для практического применения процессов квантовых блужданий частиц полезна реализация направленности блужданий. Явление, когда процесс перемещения частицы между вершинами графа в одном направлении отличается фазой от процесса перемещения в противоположном направлении, называется хиральностью.

«Хиральность, которая, в частности, приводит к нарушению симметрии относительно обращения времени, в квантовых блужданиях еще мало изучена, – говорит Леонид Федичкин. – Исследование хиральности являлось предметом нашей работы».

Ученые аналитически решили систему уравнений для квантовых блужданий по циклическим графам с учетом коэффициента декогеренции для двух крайних случаев: когда коэффициент, то есть помехи от внешнего мира, очень маленький и когда он очень большой.

«Получилось, что когда этот параметр мал, то распространение частицы по графу идет линейно, то есть процесс почти идеально квантовый, – поясняет Леонид Федичкин. – А если параметр большой, то мы наблюдаем фактически классическую диффузию. То есть мы составили систему уравнений, в которых есть один переменный параметр – уровень декогерентности. Плавно его меняя, мы как бы переходим от квантового мира к классическому, то есть обе картины мира в части блужданий частицы описываются одной и той же системой уравнений, отличаясь лишь параметром декогеренции».

Таким образом, ученым удалось математически связать квантовый мир с классическим, но в практическом использовании этих формул есть сложность. Аналитическое решение этой системы уравнений можно получить лишь для двух крайних значений параметра, но в общем случае, для промежуточного уровня декогеренции и большого количества уравнений в системе, аналитического решения, как правило, не существует, и ничего не остается, как применять громоздкие и трудоемкие численные методы.

«С помощью этих расчетов мы показали, что для квантовых блужданий есть некий определенный уровень декогеренции, который помогает частице дойти до нужного узла и там остановиться, – говорит Леонид Федичкин. – С квантовыми объектами возникает одна проблема: если квантовая частица добежала до нужного узла, то это еще половина дела. Она ведь как резиновый шарик, который кинули в лабиринт – и он будет скакать по всем коридорам. Но проблема в том, чтобы он остановился в нужном узле. А как его остановить? Оказывается, есть определенный уровень декогеренции, при котором частица пройдет определенное количество узлов, как квантовый "мячик", а затем станет классической, утратит "прыгучесть" и остановится».

Однако такие расчеты для всех конкретных графов получить довольно трудно. Даже если число вершин всего 15-20, то вариантов графов, которые можно построить, соединяя эти узлы ребрами тем или иным образом, – астрономическое количество, и все их перебрать и рассчитать нереально.

«Возьмем, к примеру, химиков, которые синтезируют новые молекулы, каждая из которых обладает определенными свойствами, но им нужно найти такую, которая обладает нужными свойствами,– приводит пример Леонид Федичкин. – Если просто перебирать все возможные варианты молекул, то и всех химиков мира не хватит для их исследования».

Поэтому задача состоит в том, чтобы научиться быстро классифицировать, к примеру, графы-молекулы на те, которые могут обладать нужными свойствами, и те, которые ими обладать в принципе не могут. Тогда круг дальнейших исследований резко сужается. Для этого нужно найти какие-то общие закономерности, которые позволяют быстро отличить графы по степени их пригодности для выполнение тех или иных задач. И российским ученым удалось сделать это.

 «В чем у нас произошел прорыв: мы начали использовать искусственные нейронные сети, которые сейчас называют искусственным интеллектом, для того, чтобы классифицировать графы, – говорит Леонид Федичкин. – В чем особенность нашего подхода: математически граф для компьютера задается матрицей смежности. Допустим, у графа есть n вершин. Какие-то вершины соединены ребрами, какие-то нет. Мы строим матрицу nxn. Если соответствующие вершины соединены, то мы в клетке матрицы ставим 1, если не соединены – 0. Это и называется матрица смежности. То есть запутанный граф в многомерном пространстве, который и изобразить-то сложно, мы переводим в таблицу нулей и единиц, в понятную компьютеру форму».

Но самое главное, исследователи поняли, что матрицу смежности можно рассматривать как... изображение. Ведь, по сути, она представляет собой квадрат, заполненный единицами и нулями. Можно считать, что это фотография или картинка на дисплее, где 1 – это черный пиксель, а 0 – белый.

«Если эти матрицы рассматривать просто как «фотографии» графов, как их образы, то для их распознавания уже создано множество программ, работающих по принципу искусственных нейронных сетей», – говорит Леонид Федичкин.

Есть программы, которые умеют классифицировать фотографии по признаку «кошка» и «собака». Для этого их обучают на массиве вручную отобранных фотографий с кошками и собаками. Как эти программы, которые называют искусственным интеллектом, производят классификацию, то есть отличают кошек от собак, никто объяснить не может, но важен результат – они быстро учатся это делать. Алгоритму показывают раз за разом фотографии с кошками и собаками и «учат» его, отмечая, ошибся он, классифицируя ту или иную фотографию, или нет. В итоге очень скоро, отыскав какие-то только ему ведомые отличия, алгоритм почти перестает ошибаться.

 

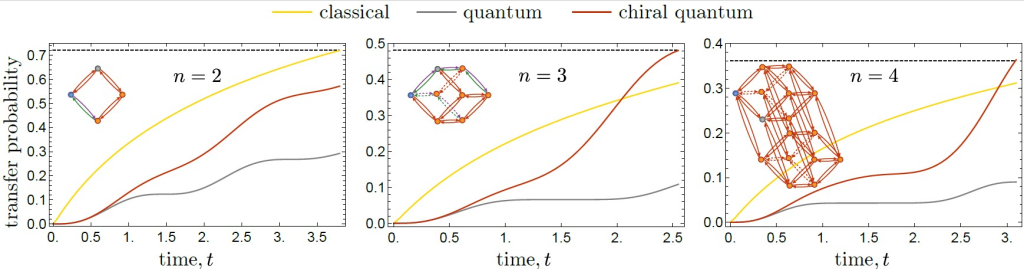
На графиках видно, что хиральные квантовые блуждания при достаточно большом времени и числе узлов обгоняют блуждания классических частиц.

«Мы применили эту же методику для классификации графов по признаку "быстрый" или "медленный", – рассказывает Леонид Федичкин. – Если матрица смежности – это образ, то компьютер может "посмотреть" на него и начать высказывать какие-то суждения о свойствах "изображенного" графа».

Обучать искусственный интеллект правильно делать суждения можно на конкретных примерах, которые можно численно просчитать по изложенной выше методике.

«Мы воспользовались тем, что у нас есть модель квантовых блужданий, то есть мы можем произвести расчет для каждого конкретного графа, причем с учетом декогерентности, а это мало кто умеет в мире, – поясняет Леонид Федичкин. – Натренировавшись на этих примерах, алгоритм начнет классифицировать и те графы, которые мы не считали. Таким образом мы решили задачу классификации графов, то есть добились того, что наша программа научилась различать быстрые и медленные графы по одному их "внешнему виду", и для этого нам не надо проводить расчеты».

Более того, ученые научили свой алгоритм классифицировать и несимметричные графы, то есть с учетом хиральности. В обычном графе частица симметрично блуждает во всех направлениях между вершинами, но это условие может нарушаться, например, в магнитном поле.

«Мы научились классифицировать и такие, несимметричные графы, то есть искусственный интеллект может давать суждения о них без прямых вычислений, – говорит Леонид Федичкин. – Причем как именно он формирует свои суждения, мы объяснить не можем. Это проблема всех технологий распознавания на основе искусственного интеллекта. Но классификатор работает: можно взять множество графов, быстро отсеять негодные для наших целей, а далее заняться расчетами оставшихся».

Квантовые блуждания важны не только для поиска молекул с нужными свойствами. Это одна из основных базовых квантовых алгоритмических процедур ускорения расчетов по сравнению с обычными вычислениями. Процедур, которые обеспечивают превосходство квантовых вычислений, очень немного. Это процедура, на которой основан знаменитый алгоритм Шора, вызвавший в свое время ажиотажный интерес к квантовым компьютерам. Еще одна процедура лежит в основе алгоритма Гровера. А третья такая процедура – квантовые блуждания.

«За счет того, что квантовые блуждания происходят быстрее, чем классические, получается квантовое ускорение вычислений применительно к некоторым потенциально полезным алгоритмам, – утверждает Леонид Федичкин. – К примеру, так можно определить, является ли функция, определенная на большом дискретном множестве точек, однозначной или нет, то есть существуют или нет такие значения аргумента, при которых значения функции равны. Это можно использовать, например, для выбора функций шифрования».

Этот алгоритм позволяет быстрее решать и многовариантные задачи логистики, когда есть множество отправных и конечных пунктов и маршрутов доставки разными способами, и на каждом шаге логистической цепочки появляются все новые и новые разветвления вариантов. Просчитать издержки каждого отдельного варианта, коих число растет экспоненциально с каждым шагом, невозможно. Нужны квантовые алгоритмы. Эта задача имеет большой практический смысл.

«Речь идет о создании алгоритма оптимизации для квантового компьютера, – подводит итог ученый. – Оптимизационная задача с практической точки зрения универсальна. Мы сделали очередной шаг в этом направлении».

 Подробнее см. Supervised graph classification for chiral quantum walks, Artem Kryukov, Roman Abramov, Leonid E. Fedichkin, Alexander Alodjants, and Alexey A. Melnikov, Phys. Rev. A 105, 022208.

Редакция сайта РАН