Ученые Института прикладной математики им. М.В. Келдыша (ИПМ) РАН разработали и запатентовали способ ситуационного терминального управления спускаемым аппаратом на рикошетирующей траектории возвращения с Луны, который позволяет не только совершить посадку с отклонением не более 2 км от расчетной точки, но и справиться с самым неблагоприятным стечением обстоятельств.

Предполагается, что перспективные российские пилотируемые корабли будут совершать посадку не в бескрайних степях Казахстана, а на территории России, в том числе и возвращаясь после лунных миссий со скоростью, близкой ко второй космической (11,2 км/с). Задача возвращения спускаемого аппарата (СА) от Луны с посадкой в заданном районе, расположенном на юге территории Российской Федерации, требует высокой точности приведения из-за ограниченности места посадки. Вместе с точностью необходимо обеспечить допустимую перегрузку для пилотируемого СА с малым аэродинамическим качеством (отношением подъемной силы к лобовому сопротивлению) и расход топлива в пределах располагаемого запаса. С учетом ограничения по перегрузке СА должен возвращаться от Луны со стороны южного полушария и входить в атмосферу Земли с околопараболической скоростью (около 11 км/с). Для возвращения в любую дату вне зависимости от взаимного положения Земли и Луны должна обеспечиваться дальность спуска (от точки входа в атмосферу до района посадки) в диапазоне 5000–10 000 км. Такие дальности, при использовании СА типа конус с аэродинамическим качеством 0,3, могут быть реализованы только посредством использования рикошетирующих траекторий спуска с двумя погружениями СА в атмосферу, разделенными внеатмосферным (баллистическим) участком.

Этот способ посадки предполагает, что летящий от Луны со скоростью около 11 км/с СА под углом приблизительно 5° входит в атмосферу Земли, погружаясь в нее до высоты точки рикошета около 55-57 км, затем вновь вылетает в безвоздушное космическое пространство, совершает полет по баллистической траектории, вновь погружается в атмосферу, уже на меньшей скорости, и совершает парашютную посадку в заданном районе. Причем отклонение от точки раскрытия парашюта на высоте 4,5 км не должно превышать 2 км.

Эта задача сложна тем, что подобные траектории очень чувствительны к разного рода возмущениям и при использовании высокоточного терминального (то есть рассчитываемого из условий достижения заданной точки) алгоритма управления большое значение имеет его адаптация к фактическим условиям движения, т.е. идентификация аэродинамических характеристик (АДХ) СА, возмущенной атмосферы и ошибки навигационной высоты.

СА на такой траектории управляется следующим образом: он входит в атмосферу под определенным углом атаки (углом продольной оси к набегающему потоку), который определяется смещенным положением его центра масс. Благодаря несимметричному обтеканию корпуса, имеющего форму усеченного конуса, возникает подъемная сила с аэродинамическим качеством около 0,3. Управление спуском с помощью изменения угла атаки требует большого расхода топлива, однако меняя с помощью двигателей управления угол крена, можно вектор подъемной силы направлять в любую сторону: вверх или вниз от направления движения, удлиняя или укорачивая траекторию, вправо или влево, управляя боковым отклонением.

Для достижения высокой точности привода к месту посадки такое управление должно быть двухпараметрическим, то есть осуществляться из условия одновременного устранения промаха в продольном и боковом направлениях. Если прогнозируемая траектория имеет перелет, то алгоритм «раскрывает» угол крена (увеличивает его по модулю и может даже перевернуть СА на 180°, чтобы направить вектор подъемной силы вертикально вниз). Если траектория имеет недолет, то алгоритм уменьшает величину угла крена в пределе до нуля, когда подъемная сила направлена вертикально вверх. При этом продольное движение СА регулируется в основном величиной угла крена, а боковое движение – переворотами по углу крена, т.е. изменением знака угла крена при сохранении его величины. Такой алгоритм позволяет уменьшить расход топлива. На первом погружении в атмосферу применяются два переворота, а на втором погружении – три переворота. Такое количество переворотов является минимально необходимым для обеспечения требуемой точности.

Интересно, что способ двухпараметрического управления для создаваемого в США нового пилотируемого корабля Orion рассматривается только в качестве перспективы. А сейчас американцами используется однопараметрический терминальный алгоритм управления PredGuid, который имеет в основе алгоритм управления корабля Apollo, использовавшегося для полетов на Луну в 1960-70 гг. Единственный параметр управления этого алгоритма – величина угла крена, которая корректируется для устранения продольного промаха. Ведь Orion предполагается сажать в океан, поэтому и требования к точности не так высоки, как в случае с российским перспективным кораблем «Орел», которому по нынешним планам предстоит садиться под Оренбургом в довольно населенной местности.

Разработка управляющего алгоритма для решения этой задачи велась в ИПМ РАН в течение 10 лет. Исходный вариант терминального алгоритма управления спуском (ТАУС) в задаче возвращения от Луны по рикошетирующей траектории рассматривался при идеальной навигации, т.е. без навигационных ошибок. Модифицированный алгоритм ТАУС-М (М – модифицированный) уже учитывает навигационные ошибки и действия «усиленных» возмущений траектории, но для создания запаса по дальности в нем занижается прогнозное аэродинамическое качество СА на 8,5 %: с 0,319 до 0,292. За счет этого создается запас по дальности для всех вариантов возмущенных траекторий независимо от фактических возмущений. Такой способ адаптации является общим.

Однако, как показали статистические, то есть проведенные для сотен сочетаний различных отклонений, испытания ТАУС-М, для 3 % возмущенных траекторий его работа приводит либо к недолету, либо к большим перегрузкам на участке второго погружения СА в атмосферу из-за необходимости компенсировать перелет. К примеру, в одном из расчетных случаев недолет в 20 км возник из-за сочетания сниженного на 10 % фактического аэродинамического качества и увеличенной на 20 % фактической плотности атмосферы. В другом случае возникла большая перегрузка (8,1g) на втором погружении в атмосферу из-за большого перелета, который появился на первом погружении вследствие сочетания увеличенного на 7 % фактического аэродинамического качества и сниженной на 20 % фактической плотности атмосферы.

Поэтому была разработана новая версия алгоритма ТАУС-МС (МС – модифицированный, ситуационный), которая и обеспечивает индивидуальную адаптацию прогнозных АДХ к фактическому аэродинамическому качеству СА на основе автономных измерений. Одновременно определяется относительная плотность атмосферы (относительно бортовой среднемесячной модели) и уточняется ошибка навигационной высоты. Такая адаптация к возмущающим факторам называется ситуационной.

Основное предназначение ситуационного алгоритма ТАУС-МС состоит в гарантированной идентификации экстремальных сочетаний возмущений (сниженное аэродинамическое качество + повышенная плотность атмосферы + большая положительная ошибка по навигационной высоте или повышенное аэродинамическое качество + пониженная плотность атмосферы + большая отрицательная ошибка по навигационной высоте) и адекватной модификации управления для исключения возможности больших недолетов/перелетов и повышенной перегрузки. Средние и малые возмущения не столь опасны, так как даже предыдущая версия общей адаптации в алгоритме ТАУС-М успешно справлялась с такими возмущениями.

Для проверки работоспособности алгоритма ТАУС-МС были проведены статистические испытания по расчету 1000 возмущенных разным образом траекторий.

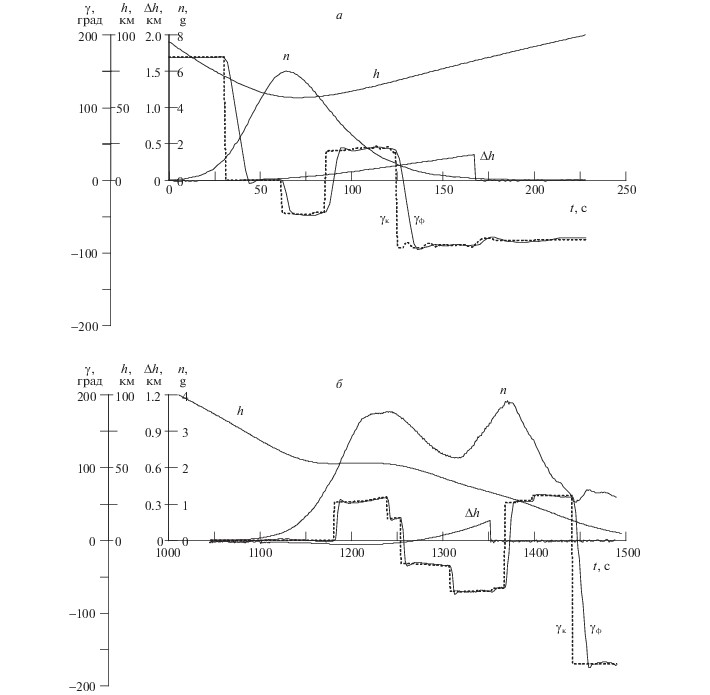
На рисунке выше приведены параметры траектории с алгоритмом ТАУС-МС (вариант № 86 из статистики 1000 псевдослучайных возмущенных траекторий): а – участок первого погружения, б – участок второго погружения, Υк и Υф – командный и фактический углы крена, h – высота, Δh – ошибка навигационной высоты, n – перегрузка.

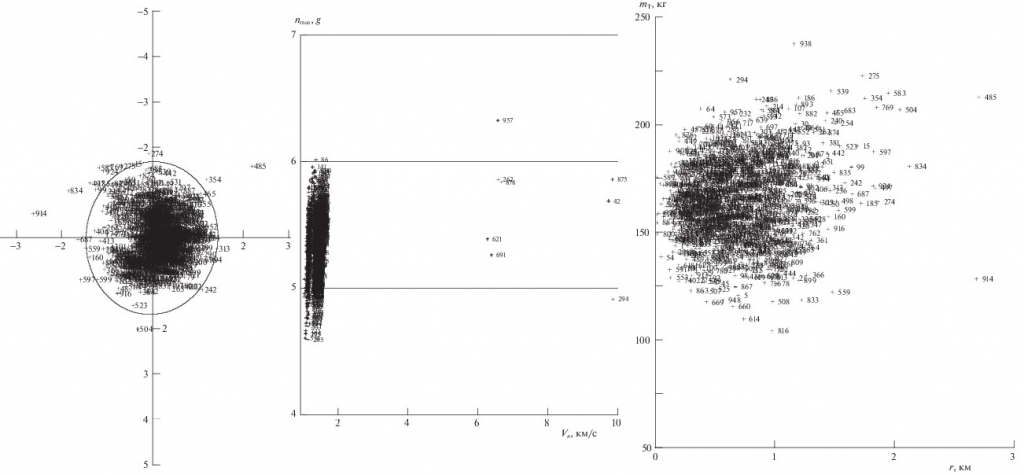
На графике вверху слева показаны координаты конечных точек (x, z) в посадочной системе координат на высоте приведения 4,5 км. Номерами обозначены варианты возмущенных траекторий. Только в трех вариантах из 1000 промах достиг 2,7 км, а в подавляющем большинстве вариантов промах меньше 2 км. На графике в середине показаны максимальные перегрузки n_max в зависимости от скорости V_n, при которой они достигаются. Только в одном варианте из 1000 перегрузка достигает величины 6,33g, а в остальных вариантах перегрузка меньше 6g. Справа показан суммарный расход топлива m_топ в зависимости от промахаr. В одном варианте расход топлива достигает 237 кг, а в остальных вариантах расход меньше 225 кг.

Статистические испытания подтвердили, что ТАУС-МС позволяет реализовать посадку СА на юге территории Российской Федерации с требуемой точностью (4 км), максимальной перегрузкой до 6g и приемлемым расходом топлива. Алгоритм ТАУС-МС защищен патентом России на изобретение.

Подробнее см. в статье «Способ ситуационного терминального управления спускаемым аппаратом на рикошетирующей траектории возвращения с Луны», А. С. Самотохин, Ю. Г. Сихарулидзе, А. Г. Тучин, «Известия РАН. Теория и системы управления», 2022, № 1, стр. 145-164.

Редакция сайта РАН