Специалисты НПО им. С. А. Лавочкина и Института прикладной математики им. М. В. Келдыша РАН рассчитали баллистическую схему, которая позволит сэкономить топливо и доставить больше груза на окололунную орбиту.

Освоение Луны потребует вывода на окололунные орбиты множества космических аппаратов (КА) навигации, связи и дистанционного зондирования, а в случае создания долговременной лунной базы потребуется организация транспортной «магистрали» Земля – Луна, частью которой может стать окололунная станция для пересадки на взлетно-посадочные лунные комплексы. В случае размещения базы на Южном полюсе Луны, где в затененных кратерах может содержаться водяной лед, целесообразно разместить такую станцию на полярной окололунной орбите с наклонением 90 градусов.

Проблема создания спутниковой группировки вокруг Луны состоит в том, что большинство окололунных орбит являются неустойчивыми из-за неравномерности гравитационного поля Луны и возмущающего воздействия Земли и Солнца. Для удержания КА на этих орбитах требуется постоянный расход топлива. В противном случае они за считанные месяцы или даже дни упадут на поверхность Луны или покинут ее орбиту.

Однако баллистиками были найдены устойчивые окололунные орбиты. Одна из них – орбита радиусом 5000 км и наклонением 90 градусов. Чтобы удержаться на такой орбите в течение 1,5 лет достаточно запаса характеристической скорости всего около 10 м/с. (Характеристическая скорость – изменение скорости космического аппарата, которое необходимо для выполнения орбитального маневра).

Российские специалисты решили задачу определения наилучшего (по критерию минимума характеристической скорости и максимума конечной массы КА на орбите Луны) перехода на эту орбиту с перелетной траектории Земля – Луна.

Рассматривался конкретный пример: КА массой 2040 кг, оснащенный двигателем тягой 420 кгс, в составе ракеты космического назначения «Союз-2.1б» с разгонным блоком «Фрегат» стартует с одного из трех космодромов (Байконур, Восточный, Куру) и выводится на промежуточную опорную околоземную орбиту высотой 200 км и с наклонением 51,6°, затем в течение 1–1,5 ч происходит пассивный полет по этой орбите. В расчетный момент времени двигательная установка разгонного блока сообщает импульс скорости, переводящий КА на траекторию полета к Луне. Далее, в течение 4,5 суток после отделения от разгонного блока КА летит к Луне.

Граница сферы преобладающего действия гравитации Луны начинается на расстоянии 60 тыс. км от центра Луны. После ее пересечения движение КА моделируется в рамках задачи гравитационного взаимодействия четырех тел – КА, Луна (с учетом ее реального гравитационного поля), Земля и Солнце (как материальные точки).

Сравнивались одно-, двух- и трехимпульсный варианты перехода с перелетной траектории на заданную орбиту Луны (радиус 5000 км, наклонение 90 градусов).

Рис. 1. Схема перелета с Земли на Луну с одноимпульсным (а), двухимпульсным (б) и трехимпульсным (в) переходом КА на круговую орбиту Луны.

Первый вариант (рис. 1, а) – это классическая траектория выведения, реализующая схему прямого перелета КА от Земли с одноимпульсным маневром торможения у Луны. В случае одноимпульсного торможения для схода КА с гиперболы подлета к Луне на целевую орбиту двигательная установка сообщает один тормозной импульс.

Известно, что одноимпульсная схема является наиболее выгодной при выходе на низкие окололунные орбиты. Дело в том, что тормозной импульс наиболее эффективен в самой близкой точке пролетной траектории к поверхности небесного тела – перицентре (в данном случае – в периселении). Однако в случае выхода на орбиту радиусом 5000 км тормозной импульс также приходится выдавать на высоте 5000 км, что снижает его эффективность. Для устранения этого недостатка была рассмотрена трехимпульсная схема.

В случае трехимпульсного варианта, который в баллистике называется биэллиптическим переходом Штернфельда (рис. 1, б), первый тормозной импульс проводится на минимально возможном с точки зрения практической реализации расстоянии в 100 км от поверхности Луны, после чего КА выходит на промежуточную эллиптическую орбиту Т1. С эллипса Т1 с периселением в 100 км необходимо перейти на эллипс Т2 с периселением в 5000 км. Для этого в наиболее удаленной точке орбиты Т1 – ее апоселении – на расстоянии 45 тыс. км от центра Луны выдается второй, разгонный, импульс, в результате чего формируется орбита Т2. Разгонный импульс, в отличие от тормозного, наиболее эффективен в самой дальней точке траектории. Третий, тормозной, импульс сообщается в периселении орбиты T2 на высоте 5000 км от центра и переводит КА на конечную полярную круговую орбиту с радиусом 5000 км.

Это кажется парадоксальным, но, несмотря на необходимость двух тормозных и одного разгонного импульса вместо одного тормозного, эта схема оказывается энергетически более выгодной для выхода на высокие орбиты.

Однако российским специалистам удалось найти алгоритм расчета еще более выгодной, двухимпульсной схемы, в которой нет необходимости проводить второй, разгонный, импульс. Дело в том, что при значительном удалении от Луны и приближении к границе ее гравитационного воздействия (60 тыс. км) возрастает возмущающее воздействие на траекторию КА Земли и Солнца, и эти воздействия можно использовать вместо разгонного импульса. Для этого необходимо таким образом рассчитать высоту наивысшей точки (апоселения) эллиптической орбиты Т1, чтобы суммарное воздействие Земли и Солнца на КА сообщило ему ускорение, необходимое для перехода на орбиту Т2. Таким образом, необходимость в разгонном импульсе для перехода с Т1 на Т2 отсутствует. В случае трехимпульсной схемы апоселений орбиты Т1 имеет высоту 45 тыс. км, а в случае двухимпульсной схемы эта высота в зависимости от даты старта меняется от 46,5 до 65,5 тыс. км. Алгоритм расчета такой орбиты гораздо сложнее, но в результате получается дополнительная экономия топлива за счет «пассивной» коррекции орбиты возмущающими факторами Земли и Солнца.

Что касается наклонения орбиты, то во всех вариантах момент подлета к Луне подбирается так, чтобы в конце, после всех маневров, получилась полярная орбита с заданным наклонением 90°. Для этого баллистиками был разработан специальный алгоритм подбора начального наклонения подлетной траектории, который позволяет не тратить топливо на изменение наклонения орбиты.

При сравнении эффективности трех этих вариантов следует учесть, что экономия топлива зависит от даты старта. Дело в том, что Луна вращается вокруг Земли не по круговой, а по немного вытянутой орбите, и расстояние от Земли до Луны меняется от 363 до 404 тыс. км. Расчеты, проведенные для разных дат подлета к Луне в 2030 году, показали, что прослеживается прямая зависимость между величинами тормозного импульса и расстоянием от Земли до Луны. Зависимости эти носят близкий к периодическому характер, их колебания почти повторяются один раз в лунный месяц (рис. 2).

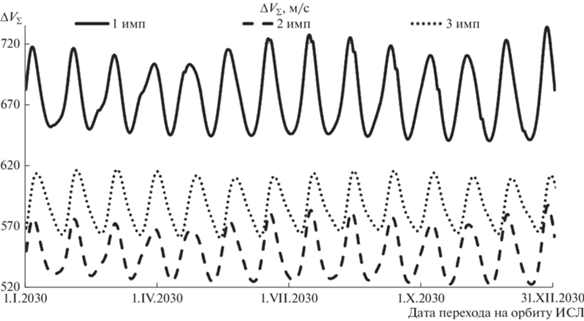
Рис. 2. Зависимости суммарной характеристической скорости для одно-, двух- и трехимпульсного вариантов торможения при переходе на конечную высокую полярную круговую орбиту радиусом 5 тыс. км от даты подлета КА к Луне в 2030 году.

Расчеты массово-энергетических характеристик трех схем показали, что выигрыш трехимпульсного выведения над одноимпульсным по суммарной характеристической скорости меняется в пределах от 79 до 116 м/с, а по конечной массе КА – от 45 до 64 кг. Выигрыш двухимпульсного выведения над трехимпульсным по суммарной характеристической скорости составляет от 29 до 35 м/с, а по конечной массе КА – от 20 до 22,2 кг. Выигрыш двухимпульсного выведения над одноимпульсным по суммарной характеристической скорости составляет от 114 до 155 м/с, а по конечной массе КА – от 65 до 86,3 кг. Для варианта с двухимпульсным торможением при переходе на указанную конечную орбиту в 2030 г. суммарная характеристическая скорость меняется в диапазоне от 525 до 577 м/с, при этом масса КА на целевой орбите варьируется от 1652,9 до 1694,8 кг.

Из полученных результатов следует, что в классе рассмотренных схем одно-, двух- и трехимпульсных перелетов на высокую круговую орбиту Луны энергетически оптимальными являются двухимпульсные перелеты. Однако у них есть свои недостатки. В случае двухимпульсного торможения длительность переходного маневра, в зависимости от даты старта, изменяется в пределах от 4,2 до 8,1 суток, а при трехимпульсном – остается практически постоянной, не превышая 4 суток.

Кроме того, выполненный анализ учитывает только номинальное движение КА и не учитывает ошибки управления и навигации и необходимость проведения коррекций для их компенсации. Из-за большой чувствительности двухимпульсных траекторий к действующим на КА возмущениям, расход топлива на подобную коррекцию окажется, возможно, больше, чем для более устойчивого трехимпульсного выведения, что, в целом, может сократить выигрыш двухимпульсного варианта выведения в сравнении с трехимпульсным. В связи с этим возникает необходимость дальнейшего анализа задачи, в частности, с учетом коррекций для парирования ошибок управления и навигации при полете КА на заключительном этапе перелета на орбиту Луны.

Подробнее см. «Анализ траектории выведения космического аппарата на высокие круговые орбиты искусственного спутника Луны», Е. С. Гордиенко, В. В. Ивашкин, А. В. Симонов, П. Е. Розин, «Космические исследования», 2022, т. 60, № 3, стр. 235-245.

Редакция сайта РАН