Одним из самых значимых для России событий на прошедшем в июле 2022 г. Международном конгрессе математиков стало вручение премии Лилавати за выдающийся вклад в популяризацию математики российскому ученому, создателю проекта «Математические этюды» Николаю Андрееву. Мы попросили его рассказать об этом событии, а также о работе Лаборатории популяризации и пропаганды математики, которую он возглавляет в Математическом институте им. В. А. Стеклова РАН (МИАН).

Николай Николаевич, ваш проект «Математические этюды» широко известен в стране, у него немало наград и отличий на национальном уровне, а премия Лилавати означает и его международное признание. Насколько это важно?

У России не так много премий Международного математического союза, а это высшая награда в нашем сообществе, и, конечно, получить ее очень почетно. Но, на мой взгляд, это не только признание нашего проекта, а вообще признание традиций и вклада нашей страны в популяризацию математики. В изданной в рамках нашего проекта книге «Математическая составляющая» есть глава «Книжная полка» со списком самой интересной литературы по математике. Приходилось очень тщательно отбирать книги для нее, потому что действительно в России в разное время было издано очень много очень качественной научно-популярной литературы.

И хотя в нашем проекте мы начали использовать трехмерную компьютерную графику, но при этом мы пытаемся сохранить главную особенность традиционного российского подхода к популяризации, который состоит в том, что надо не только показать какой-то фокус, но и чему-то научить. У нас одно время даже возник лозунг: новые формы традиции.

Международное признание – это важный шаг, так как мы в основном работали в России, к примеру, все лекции проходили на русском. Тем приятнее, что эту работу оценили и за рубежом. Перед вручением премий происходит представление лауреатов, и нас представлял, на мой взгляд, лучший популяризатор математики современности – Тадаши Токиеда из Стэнфорда. Я очень рекомендую всем найти записи его выступлений в «ютубе». Его лекции всегда очень интересны, его образованность – и общекультурная, и математическая – не знает границ.

Главная станица сайта «Математические этюды».

Есть ли планы в связи с этим успехом развивать проект за рубежом?

На самом деле сайт «Математические этюды» частично переведен на английский язык, и не только на английский, но и на французский и итальянский, и будет переводиться и дальше. Что касается его зарубежных перспектив, то тут все просто: настолько качественный материал появляется крайне редко и, конечно же, он ценен на всех языках.

Насколько повлияла на обстановку во время конгресса политическая ситуация?

Конечно, если бы конгресс проходил в Санкт-Петербурге, как изначально планировалось, было бы куда больше внимания и внутри страны, и за границей, тем не менее, я надеюсь, что по прошествии некоторого времени ситуация наладится. Математикам повезло, потому что теоремы, будучи доказанными, не меняются от политических взглядов, поэтому во все времена математика становилась мостиком между островами непонимания в мире. Хочется надеяться, что так будет и впредь.

Один из 71 анимационного фильма проекта «Математические этюды».

С чего начинался ваш проект и как возникла Лаборатория популяризации и пропаганды математики в МИАНе?

Мы занялись популяризацией математики еще в 2002 году, и премия в каком-то смысле подарок нам к 20-летию. Первые компьютерные фильмы были сняты по научным задачам, которыми я занимался. Когда стало понятно, что они вызывают большой интерес как в научной среде, так и в среде учителей и школьников, мы решили продолжать эту работу, и в 2010 году, по инициативе и при поддержке тогдашнего нашего директора Валерия Васильевича Козлова, была создана лаборатория – небольшая, но важная по двум причинам.

Во-первых, про науку хорошо может рассказать только человек, ее понимающий. Надо знать намного больше того, о чем рассказываешь, чтобы иметь возможность из этого знания отобрать то, что полезно узнать неподготовленному человеку. А второй аспект заключается в том, что в эту комнату, где расположена наша лаборатория, приходят многие сотрудники института и делятся своими идеями о том интересном, что они узнали в мире науки. И мы стараемся их использовать для популяризации.

Важно, что таким образом мы вводим в мир популяризации новые идеи. Нарисовать красивые картинки ко всем известной «Занимательной математике» Якова Исидоровича Перельмана могут и без нас, хотя без математической подготовки даже это сделать невозможно. Отдельная заслуга Романа Кокшарова, художника-оформителя всех наших проектов и, в частности, книги «Математическая составляющая», что все его картинки математически точно выверены. То же самое относится и к фильмам на нашем сайте «Математические этюды». В них все правильно складывается, раскладывается и перемещается с точки зрения математики, и это очень важно, потому что, во-первых, не вводит в заблуждение, а во-вторых, – в популяризации науки все должно быть честно. Все, что ты говоришь, должно быть правдой. Ты можешь не говорить всю правду, потому что некоторые вещи очень сложно объяснить, но то, о чем говорится, должно быть правдой, включая картинки.

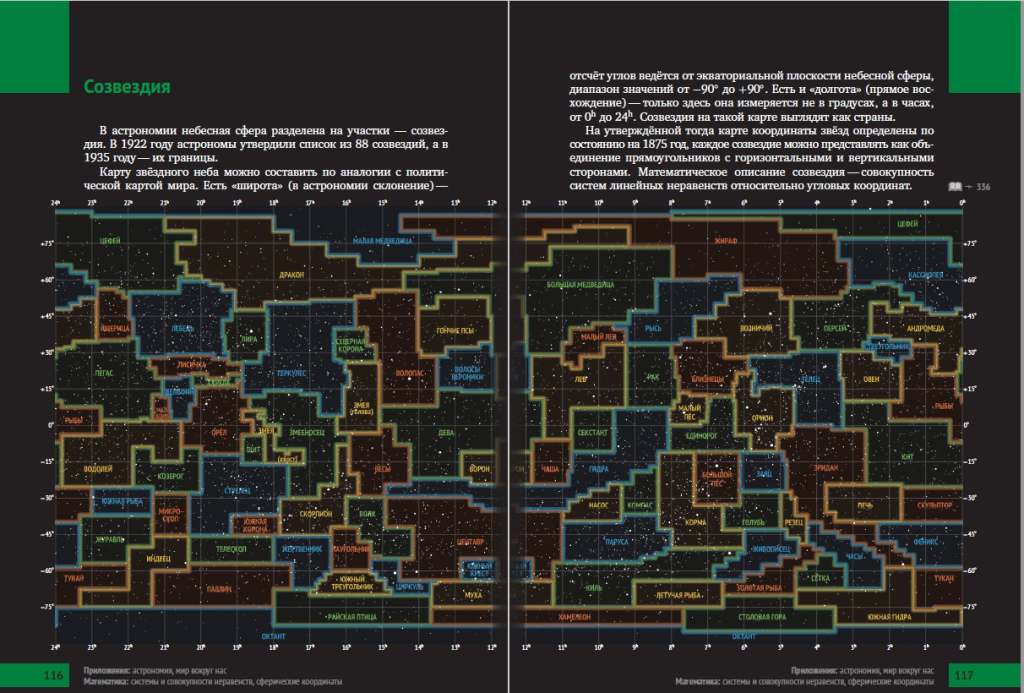
Один из разворотов книги «Математическая составляющая».

Вы сказали, что первые анимации появились из ваших математических работ. Это было их частью?

Нет, конечно, это не было каким-то научным математическим исследованием. Просто показалось, что ту задачу, которой я занимался, можно более понятно и доступно даже неподготовленному человеку представить в виде компьютерной анимации. И вскоре выяснилось, что это действительно так.

А что это были за задачи, которые впервые навели вас на идею о компьютерной анимации?

На самом деле эти задачи очень близки к тому, за что Марина Вязовская в этом году получила Филдсовскую премию. Она решила задачу об упаковке шаров в 8- и 24-мерном пространстве. Я занимался близкими задачами. Одна из них – задача Томпсона о расположении электронов на сфере, когда вы бросаете несколько электронов, которые отталкиваются друг от друга, но при этом им запрещено покидать сферу, и нужно найти конфигурацию их расположения с минимальной потенциальной энергией системы. А вторая задача – это задача о контактном числе шаров. У вас есть шар, и надо понять в разных размерностях, как много таких же шаров могут касаться центрального. На самом деле это очень практическая задача о сферических кодах, исправляющих ошибки. Первые фильмы были сняты в качестве пояснения этих работ, именно они положили начало нашему проекту, хотя сейчас пересматриваем их с улыбкой, потому что с тех пор в техническом плане мы сильно продвинулись.

Одна из первых трехмерных анимаций проекта была посвящена решению задачи Томпсона.

В чем этот прогресс выражается?

Все-таки накоплен уже большой опыт, выработался стиль подачи. Проведено больше тысячи лекций в совершенно разных аудиториях, чаще всего среди школьников и учителей, причем не только из каких-то спецшкол. Смотришь на их реакцию, иногда понимаешь, что здесь нужно показать по-другому. Мы, как правило, сначала обкатываем наши фильмы на лекциях, как-то их меняем, а потом уже выкладываем в открытый доступ на сайт «Математические этюды». Относительно недавно, около полутора лет назад, завели страничку «ВКонтакте» и ввели там математические вторники, когда каждую неделю в этот день появляется что-то новенькое.

Мы делаем не только виртуальные вещи для интернета, но и материальные наглядные пособия. Мечтали – и продолжаем мечтать – подарить наши модели во все школы, но для этого нужны большие финансы. А пока мы открыли проект «Математическая модель – в школу!»: если школьник сам или с родителями делает какую-то модель и дарит ее школе, то мы ему в подарок посылаем нашу книгу «Математическая составляющая». Видимо, это заинтересовало детей, и одну-две книги в неделю в течение учебного года мы высылаем в ответ на присланные фотографии сделанных для школ моделей. Хочется, чтобы математические кабинеты начинали наполняться наглядными пособиями. Это, понятное дело, не произведет революции в образовании, но поможет сделать некий небольшой шажок к тому, чтобы дети и лучше понимали математику, и им было интереснее учиться, а когда есть интерес, то это залог хорошего изучения предмета.

Николай Андреев мечтает подарить свои математические модели всем школам.

Популяризация – актуальная проблема для любой науки, но что-то я не слышал, чтобы в других институтах РАН создавались лаборатории по популяризации физики, химии или электроники. Почему в Математическом институте руководство решило создать такое подразделение?

Вы знаете, Валерий Васильевич Козлов, ныне академик-секретарь Отделения математических наук РАН, а в те годы – директор МИАНа, очень много сделал и для развития института, и для науки. В вопросе создания Лаборатории популяризации также свою роль сыграли его чутье и видение проблемы. Важность, которую он придавал созданию лаборатории, подчеркивает тот факт, что у нас вообще-то институт небольшой по сравнению с другими, хотя по числу членов академии наук, работавших и работающих в этих стенах, он, если не ошибаюсь, лидирует: на 150 сотрудников у нас 15 академиков и 17 членов-корреспондентов РАН.

В этом смысле премию можно считать еще одним подтверждением того, что идея создания лаборатории полностью себя оправдала. Ведь, по большому счету, каких только наград у нашего проекта нет, включая Премию Президента РФ в области науки и инноваций, Золотую медаль РАН и теперь вот премию Лилавати. Надеемся, что этот пример покажет, что и в других институтах можно и нужно создавать подобные структурные подразделения. Конечно, не стоит сравнивать занятия наукой и популяризацию науки, но это тоже важное и нужное дело, на которое требуется много сил и времени, и хочется, чтобы тем сотрудникам, которые умеют это делать – и лекции читать, и материалы готовить – это шло в некоторый зачет по работе.

Вы говорили, что рассказать хорошо о науке может только ученый, но у меня был случай, когда один математик на мою просьбу популярно изложить суть его работы, отмеченной академией наук, откровенно ответил, что, к сожалению, это абсолютно невозможно. Получается, что математика может понять только математик?

Действительно, есть области, которые объяснить широкой публике невозможно. Более того, есть области математики, которые я сам, например, не понимаю и поэтому не берусь их объяснять, потому что порог вхождения там такой, что надо много лет поработать, прежде чем ты сможешь хотя бы что-то про эти области рассказать. Но я и не утверждал, что в математике можно объяснить все что угодно. Я говорил, что качественно объяснить математику может только математик. Более того, всегда приятно, когда сам специалист рассказывает о своей работе, иначе получается некая вторичность, а уж когда берутся за объяснения журналисты, то получается совсем грустно. И мы, кстати, это учитывали в нашей книге «Математическая составляющая», где есть три части: самая простая, про проявления математики в каждодневном быту, она написана сотрудниками лаборатории Никитой Панюниным, Сергеем Коноваловым и мной, а две остальные части содержат авторские статьи ведущих математиков страны, и получить такое объяснение из первых рук – очень важно и полезно.

В чем специфика популяризации именно математики?

Математика отличается тем, что имеет дело в основном с абстрактными понятиями. Физики или химики могут провести наглядную демонстрацию своих опытов, показать оборудование, продемонстрировать результаты экспериментов – и аудитория будет впечатлена, а математикам еще надо придумать, как, помимо непонятных формул, объяснить абстрактные вещи. В этом, собственно говоря, главная сложность, поэтому одно из основных направлений деятельности нашей лаборатории – это создание наглядных математических моделей в виде компьютерной анимации или в физическом виде.

Вторая сложность состоит в том, чтобы выбрать математические сюжеты, которые можно красиво показать. Ведь и стандартную теорему Пифагора из школьной программы можно подать, как это сделали мы, в виде головоломки, которая, кстати, пользуется большой популярностью, но чтобы сделать это, опять-таки, нужно знать много чего помимо школьной программы.

Технологии не стоят на месте. Все более популярными становятся, например, компьютерные игры. Собираетесь ли развивать проект в этом направлении?

Мы всегда пробуем что-то новое. Интересный опыт – это создание приложений под мобильные устройства. В конце 2011 года мы впервые выпустили приложение «В уме», которое можно найти в магазине приложений App Store. Это интерактивная реализация задачника «1001 задача для умственного счета» великого русского педагога XIX века Сергея Александровича Рачинского. Интересно, что в позапрошлом веке деревенские дети могли такие задачи решать в уме, а современному человеку надо очень попыхтеть, чтобы справиться с ними.

Эта программа получила огромную популярность, и в какой-то момент вышла на первые места в главном рейтинге App Store и довольно долго там продержалась. Ее скачали миллионы пользователей. И это пример того, что современные устройства при правильном использовании могут быть каналом для традиционных способов популяризации науки. Еще упомяну программы по геометрии «Евклидия» и «Пифагория», сделанные коллегами из Санкт-Петербурга и также пользующиеся популярностью.

Но нет ли проблемы в том, что внимание сегодняшних детей надо привлекать чем-то все более и более визуально зрелищным? Ведь все время появляются новые гаджеты, вроде очков виртуальной реальности.

Когда в 2002 году мы начали использовать трехмерную компьютерную графику, она действительно была в новинку и сама по себе стала мощным инструментом привлечения внимания, но дальше уже требуется некое искусство, чтобы, завладев вниманием, ты мог рассказать что-то интересное и полезное о математике, так что к одной только зрелищности дело не сводится. Если говорить о виртуальной реальности, то пока я в ней чего-то интересного для математического преподавания не вижу. Если делать качественно, то не всегда обязательно гнаться за модой или за внешними эффектами, и в подтверждение этого я приведу два примера.

Начинали мы с компьютерной графики, а потом пришли к книге «Математическая составляющая», но мы сделали ее очень качественно, и она разошлась огромным тиражом несмотря на то, что выложена бесплатно в интернете. Ведь это отдельное удовольствие – посидеть и подумать над книжкой.

А второй пример – это журнал «Квантик», потрясающе оформленный ежемесячный журнал для любознательных, причем далеко не только школьников. Я и для себя нахожу в нем много интересного. Это журнал успешный, его выписывают. Все знакомые дети, когда приносишь им «Квантик», так и застывают с ним там, где его получили. А еще в нем до сих пор сохранился традиционный жанр переписки с читателями, а именно – проводится ежемесячный конкурс, публикуются задачи, дети их решают, пишут в редакцию, а редакция им отвечает, что правильно решено, а что неправильно. Этот опыт показывает, что содержание важнее формы. Вопрос качества гораздо более важен, чем участие в гонке за современными технологиями.

Обложки журнала «Квантик».

Почему в ваших анимированных этюдах нет звука?

Потому что они рассчитаны на вдумчивый просмотр, который иногда нужно останавливать, чтобы прочитать поясняющую статью. Познание требует полной сосредоточенности и своего темпа. Этому даже фоновая музыка помешает. Кроме того, эти фильмы рассчитаны на показ в совершенно разных аудиториях, кому-то надо просто показать и поверхностно рассказать, а кому-то можно на основе фильма сделать научный доклад. Здесь звук только мешал бы, потому что каждый лектор может рассказывать по-своему.

В интернете есть много записей моих лекций, где я показываю фильмы и очень часто останавливаю их, чтобы сделать небольшие – или большие – отступления в зависимости от реакции аудитории. Эти фильмы – некая универсальная вещь, и, кстати, как раз это и было отмечено в представлении на премию, с которым выступил Тадаши Токиэда. Он говорил, что это материал, который каждый может использовать по своему усмотрению. Наши фильмы и наши модели дают некий широкий набор возможностей для их использования в самых разных ситуациях.

Один из интересных проектов лаборатории – создание моделей механизмов Чебышёва.

Компьютеры уже побеждают людей в шахматы, пишут стихи, сочиняют музыку, рисуют картины. Возможно, что скоро искусственный интеллект заменит, к примеру, журналистов. А сможет ли он когда-нибудь заменить математиков?

Журналистов, может, и заменит, но математиков уж точно нет. Даже учителя математики не заменит, потому что при обучении человеческое общение с детьми очень важно. Нельзя просто поставить телевизор в классе и запустить какую-то говорящую голову по трансляции, хотя мы, к сожалению, к этому идем, но это будет конец образованию. Ведь одно дело, когда все эти материалы просто лежат на сайте, пускай даже ими много кто пользуется, а другое – настоящие лекции, когда я приезжаю в разные города и все это показываю. Удается заинтересовать тех школьников, которые сами никогда бы на этот сайт не зашли и на нашу книгу не посмотрели. Увлеченные математикой сами посмотрят наши этюды, а вот изменить отношение тех, кто считает эту науку неинтересной, – и есть наша задача.

Учитель – это человеческое общение, которое компьютер не заменит, но почему искусственный интеллект не сможет заменить математика?

Не заменит, потому что перед тем, как решить задачу, надо ее выбрать и поставить, а это может сделать только человек. Математика не сводится к механическому выводу одной формулы из другой. Математика – это понимание мира и того, как он устроен. И с этой задачей, кроме человека, никто не справится, да и человечеству все время своего существования еще думать над этим.

Вы используете в популяризации такие факторы, как красота математики, ее философия?

Красота и философия – это разные вещи. На самом деле музыка основана на математике, чему посвящена отдельная глава в «Математической составляющей». Очень много математики в гравюрах Мориса Эшера. Что касается философии математики, то, как я уже говорил, в разделе «Книжная полка» в той же книге «Математическая составляющая» мы привели список литературы, которая была бы полезна в школьных кабинетах математики, но вообще-то там есть много чего интересного почитать и взрослым. В их числе три книги, которые появились не так давно, уже после советских времен, славных обилием хороших книг по математике. Это книга нашего великого ученого и популяризатора Владимира Игоревича Арнольда, которая называется «Математическое понимание природы», книга Владимира Андреевича Успенского «Апология математики», и, собственно, почему я вспомнил про этот список, в нем есть книга нашего великого математика Юрия Ивановича Манина, которая называется «Математика как метафора». К этой книге я и отсылаю тех, кто интересуется философией математики.

Я очень рад, что Юрий Иванович принял участие в создании нашей книги. Его статья в ней называется «Математика – язык описания возможностей». Она заканчивается следующими словами: «Математика описывает фазовые пространства реального мира – пространства возможностей. Она изучает законы, которые определяют возможные траектории в этом фазовом пространстве, а также условия – тот набор информации, который необходим для выбора конкретной фазовой траектории». То есть математика дает человечеству не только конкретные инструменты, но и действительно в некотором смысле говорит о том, куда оно может двигаться.

Беседовал Леонид Ситник, редакция сайта РАН.

Фото Елены Ситник

Читайте также «Лев Беклемишев о премии Лилавати Николаю Андрееву»